Topic:- Arithmetic progressions
Arithmetic progression (A.P.) is a sequence of numbers such that the difference of any two successive members of the sequence is a constant. For instance, the sequence 3, 5, 7, 9, 11, 13... is an arithmetic progression with common difference 2.
If the initial term of an arithmetic progression is a1 and the common difference of successive members is d, then the nth term of the sequence is given by:
Question:-
Given that 5 th term and 12 th term s of an arithmetic progression are 11 and 25 respectively .find "a" and "d".
Solution:-
Given 5 th term = 11
a+4d = 11 ----1
Given 12 th term = 25
a+11d=25 -----2
Subtract 1 from 2
a + 11d = 25
a + 4d = 11
(-)
-------------------
7d = 14
d = 2
Substitute d=2 in 1
a + 4d = 11
a + 4(2)= 11
a + 8 = 11
a = 11-8
a = 3
For more help on this ,you can reply me.
Arithmetic progression (A.P.) is a sequence of numbers such that the difference of any two successive members of the sequence is a constant. For instance, the sequence 3, 5, 7, 9, 11, 13... is an arithmetic progression with common difference 2.
If the initial term of an arithmetic progression is a1 and the common difference of successive members is d, then the nth term of the sequence is given by:
Question:-
Given that 5 th term and 12 th term s of an arithmetic progression are 11 and 25 respectively .find "a" and "d".
Solution:-
Given 5 th term = 11
a+4d = 11 ----1
Given 12 th term = 25
a+11d=25 -----2
Subtract 1 from 2
a + 11d = 25
a + 4d = 11
(-)
-------------------
7d = 14
d = 2
Substitute d=2 in 1
a + 4d = 11
a + 4(2)= 11
a + 8 = 11
a = 11-8
a = 3
For more help on this ,you can reply me.

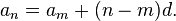
No comments:
Post a Comment